Data Structure & Algorithm/알고리즘(Algorithm)
09. 그래프 탐색
jihyeon99
2024. 7. 10. 15:01
1. 그래프 (Graph)
그래프의 정의
여러 개의 노드(node)와 이들을 연결하는 간선(edge)으로 이루어진 자료구조로, 관계를 추상적으로 표현한 구조입니다.
예를 들어, 정점은 SNS라면 각각의 유저를, 지하철 노선도라면 역을 의미하고, 관계는 SNS라면 팔로우 관계를, 지하철 노선도라면 역과 역을 잇는 길을 의미합니다.
그래프의 분류
그래프는 방향성과 가중치 유무 등에 따라 몇 가지 유형으로 나뉩니다.
- 방향성에 따른 분류
- 무방향(Undirected) 그래프 : 간선에 방향이 없는 그래프입니다. 즉, 그래프 내 모든 길을 양방향으로 이동할 수 있음을 의미합니다.
- 방향(Directed) 그래프 : 간선에 방향이 있는 그래프입니다. 즉, 그래프 내 한쪽 방향으로만 갈 수 있는 길이 하나라도 있음을 의미합니다. 차수를 부를 때, 들어올 수 있는 정점의 수와 나갈 수 있는 정점의 수가 다르기 때문에, 진입차수(In-degree)와 진출차수(Out-degree)로 구분해서 부릅니다.

- 가중치 유무에 따른 분류
- 가중(Weighted) 그래프 : 간선에 가중치가 부여된 그래프입니다.
- 비가중(Unweighted) 그래프 : 간선에 가중치가 없는 그래프입니다.

- 연결 관계에 따른 분류
- 연결 그래프 : 그래프의 모든 정점이 서로 연결되어 있는 그래프입니다. 즉, 어떤 두 정점을 잡아도 갈 수 있는 경로가 존재하는 경우를 말합니다.
- 비연결(단절) 그래프 : 그래프의 일부 정점이 서로 연결되어 있지 않은 그래프입니다. 즉, 어떤 두 정점 사이에 경로가 존재하지 않는 경우가 하나라도 있는 경우를 말합니다.

- 사이클 여부에 따른 분류
- 특정 지점에서 출발해서 다시 본래 지점으로 돌아올 수 있다면, 그래프에 사이클 (Cycle)이 있다고 합니다.

그래프의 구현
그래프를 구현하는 방식은 인접 행렬과 인접 리스트 크게 두가지가 있습니다.
각 구현 방법에 대해 설명하기에 앞서, 정점의 수는 |V|, 간선의 수는 |E|라고 정의하겠습니다.
- 인접 행렬 이용
- |V| x |V| 크기의 2차원 배열을 만들어서 연결 관계를 표현하는 것입니다.
- A → B로 가는 길이 있다면 배열의 값을 1로, 가는 길이 없다면 배열의 값을 0으로 지정합니다.
- 시간복잡도
- 특정 정점 I, J가 연결되어 있는지 확인하는데 O(1)가 소요됩니다.
- 특정 정점과 연결되어 있는 모든 정점을 확인하는데 O(|V|)의 시간이 소요됩니다.
- 특정 정점과 연결된 정점의 수를 확인하는데 O(|V|)이 소요됩니다.
- 공간복잡도는 모든 정점쌍의 연결상태를 연결 여부와 관계 없이 저장해야하므로 O(|V| * |V|)가 소요됩니다.

- 인접 리스트 이용
- |V|개의 연결 리스트를 만들고, 연결 리스트에 특정 정점과 인접해있는 정점들의 정보를 담는 것입니다.
- A → B로 가는 길이 있다면, A 정점과 관련된 연결리스트에 B 정점을 추가합니다.
- 시간복잡도
- 특정 정점 I, J가 연결되어 있는지 확인하는데 O(min(degree(I), degree(J))가 소요됩니다.
- 특정 정점 X와 연결되어 있는 모든 정점을 확인하는데 O(degree(X))의 시간이 소요됩니다.
- 특정 정점과 연결된 정점의 수를 확인하는데 리스트의 크기를 확인에 O(1)이 소요됩니다.
- 공간복잡도는 각 노드에 대해 연결된 인접 정점들만 담아주면 되므로 O(|V| + |E|)가 소요됩니다.

그래프 문제를 풀때는 정점개수 대비 간선개수를 생각해 봅니다. 입력으로 들어온 간선수(E)와 최대 간선수(V*(V-1)/2)를 비교하여, 인접행렬과 인접리스트 중 더 유리한 것을 사용합니다.
- 보통 최대 간선수의 절반(1/2)보다 작으면 희소그래프이므로, 인접리스트가 유리합니다.
- 보통 최대 간선수의 절반(1/2)보다 크면 밀집그래프이므로, 인접행렬이 유리합니다.
2. DFS 탐색 (Depth First Search; 깊이 우선 탐색)
개념
- 최대한 깊게 탐색한 후 더 이상 도달할 수 없는 상황이라면 다시 이전으로 돌아갑니다.
- 재귀를 활용해 DFS를 구현하는 경우가 많습니다.
- 방문할 수 있는 지점이 있다면 그 지점을 방문하는 함수를 재귀적으로 호출하고, 더 이상 방문할 곳이 없다면 함수를 종료하면 됩니다.
- 이때, 이전에 방문했던 지점은 다시 방문하지 않도록 하는 처리를 위해 visited 배열을 사용합니다.
function dfs(pos)
visit(pos)
for children of pos
if visited[child] == false
dfs(child)
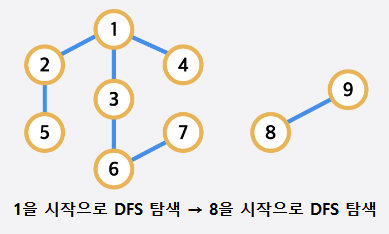
연결 요소가 여러 개인 경우, 모든 정점을 DFS 탐색
- 먼저 1번 정점을 시작으로 하여 DFS를 진행합니다.
- 이후에는 아직 방문하지 않은 정점 중 번호가 가장 낮은 지점을 시작으로 다시 DFS 탐색을 진행합니다. 이 과정을 모든 정점을 방문할때까지 반복합니다.
3. BFS 탐색 (Breadth First Search; 너비 우선 탐색)
개념
- 시작점을 기준으로 가장 가까운 정점부터 차례대로 방문하게 됩니다.
- 큐를 사용하여 BFS를 구현합니다.
- 큐에서 하나의 노드를 꺼내어 방문하게 되면, 그 노드와 인접한 노드 중 방문한 적이 없는 다른 노드를 모두 큐에 넣습니다. 큐는 FIFO 구조이므로, 처음 넣었던 노드의 이웃 노드를 순차적으로 방문하게 될 것입니다.
- 이때, 이전에 방문했던 지점은 다시 방문하지 않도록 하는 처리를 위해 visited 배열을 사용합니다.
function bfs(pos)
set Q = Queue
Q.push(pos)
visit(pos)
while Q is not empty
set node = Q.pop()
for children of node
if visited[child] == false
visit(child)
Q.push(child)
DFS와 BFS의 성능 비교
- 이론상 모든 노드와 엣지를 방문하는 것이기 때문에, 시간복잡도 자체는 O(|V| + |E|)로 별 차이가 없습니다.
- 그러나 실제로 코드를 짜게되면, 재귀함수의 오버헤드(함수를 동작시킬 때 발생하는 약간의 지연 시간)때문에 DFS가 약간 느린 편입니다.
4. 가중치가 동일한 그래프에서의 최단거리 = BFS 탐색
가중치가 동일한 최단거리 문제 풀이
지점 S 출발하여 지점 E 도착하는 방법 중 가장 짧은 방법의 길이는?
가중치가 전부 동일한 그래프에서의 최단거리는 BFS를 이용하여 구합니다.
(방향 그래프에서도 동일하게 적용됩니다.)
각각의 노드간의 거리를 1이라고 가정하겠습니다.
- S에서 방문을 시작하여 이웃 정점을 큐에 넣게 되면, 큐에 있는 모든 정점은 S와의 거리가 1이 될 것 입니다.
- 마찬가지로, 1의 이웃들이 큐에 들어가게 된다면 1과의 거리가 1이므로, 자연스럽게 S와의 거리는 2가 될 것 입니다.
- 이런식으로 진행하게 되면, 자연스럽게 E에도 방문하게 되어 S와 E 사이의 거리를 구할 수 있습니다.